Диагональный метод – несостоятельный прием доказательства, изобретенный Георгом Кантором 7 декабря 1873 года.

Диагональный метод заключается в следующем:

1) принимается, что  aⁿ = n при бесконечном n (где a и n натуральные числа; a ≥ 2);

2) из этого выводится некоторое противоречие;

3) однако это противоречие объясняется НЕ тем, что невозможно aⁿ = n при указанных условиях;

4) а вместо этого делается вывод о какой-то посторонней вещи, не имеющей отношения к подлинной причине противоречия.

В широко известной литературе встречаются три разновидности Диагонального метода, обозначенные ниже как «Стягивающиеся интервалы», «Диагональный процесс» и «Диагональный элемент». Возможно, в менее известной литературе можно встретить еще и другие варианты диагонального метода.

Стягивающиеся интервалы

Именно этим вариантом Георг Кантор в письме к Рихарду Дедекинду от 7 декабря 1873 года впервые «доказал» несчетность множества действительных чисел. До этого в письме от 29 ноября он установил счетность множества рациональных чисел, Дедекинд в ответном письме показал счетность множества алгебраических чисел, и, вот, теперь 7 декабря происходит «историческое событие»: впервые миру открывается существование «несчетного множества».

Кантор взял произвольный интервал действительных чисел (b, c), предположил, что числа в нем перенумерованы в последовательности a₁, a₂, ..., a_n, ..., потом разделил интервал на три части, далее взял ту часть, в которой нет числа a₁ (на три, а не на две части делилось, видимо, для того, чтобы наверняка существовал интервал без этого числа даже в том случае, если это число пограничное между двумя другими интервалами), потом эту часть опять разделил на три части, взял интервал, в котором нет числа a₂, и т.д.: – перебирая все пронумерованные числа, образовал последовательность стягивающихся интервалов (b_i, c_i): b₁ ≤ b₂ ≤ b₃ ≤ ... ≤ c₃ ≤ c₂ ≤ c₁. Общая точка (предел) этих интервалов (по мнению Кантора, с которым согласился Дедекинд и вслед за ними многие другие) тогда и представляет собой действительное число, не входящее в пронумерованную последовательность a₁, a₂, ..., a_n, ..., и, таким образом, действительные числа перенумеровать нельзя.

Этот способ доказательства в литературе тоже причисляется к «Диагональному методу», хотя никакой диагонали тут в общем-то не видно.

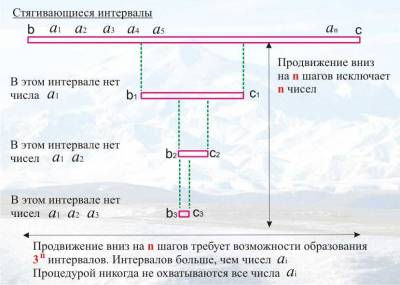
Чтобы понять сущность этого «доказательства», необходимо сначала промоделировать его на конечных последовательностях, а потом посмотреть, что будет происходить, когда n → ∞. Предположим, что пронумерованная последовательность состоит всего из 9-ти чисел: a₁, a₂, ..., a₉. Тогда на первом шаге процедуры Кантора он разделяет эту последовательность на 3 части (в каждой оказывается, допустим, 3 числа), берет одну часть, в которой нет числа a₁ (допустим, вторую); на втором шаге он разделяет эту часть опять на 3 части (в каждой теперь оказывается только 1 число), берет ту часть, в которой нет числа a₂ (допустим, первую часть, содержащую число a₄); на третьем шаге... Кантор хочет разделить эту часть на три части, но ему уже нечего делить! Процедура останавливается: Кантор перебрал только два числа из девяти, а возможности образования стягивающихся интервалов уже исчерпаны! Это и понятно: ведь в пронумерованной последовательности имеется n чисел, а для проведения процедуры Кантора требуется возможность образования 3ⁿ интервалов.

При n = 9 (девять элементов в пронумерованной последовательности) Кантор смог охватить своей процедурой лишь 2 элемента или примерно 22 %. Когда n возрастает, доля охваченных элементов всё уменьшается. Так при n = 27 он охватит примерно 11 %; при n = 81 лишь неполных 5 % и т.д. (Некоторые коррекции вносят случаи, когда деление интервала производится не на равные части, но общий принцип и в таком случае сохраняется). В предельном случае доля охваченных процедурой Кантора элементов среди всех элементов стремится к нулю. (По правилу Лопиталя предел неопределенности n/3ⁿ при n → ∞ есть 0).

Оригинальное доказательство Кантора со стягивающимися интервалами в наше время упоминается редко, а «несчетность действительных чисел» обычно «доказывается» при помощи Диагонального процесса (тоже изобретенного Кантором, но в другой связи).

Диагональный процесс

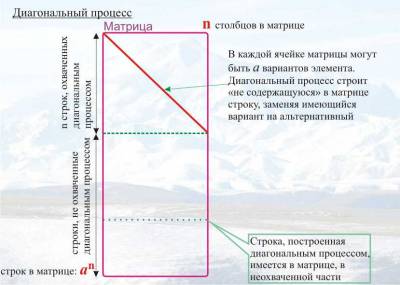
Диагональный процесс – это процедура, которая проводится в матрице, имеющей ширину n столбцов, а дину aⁿ строк. Матрица состоит из элементов, имеющих a разновидностей. В начале рассуждения предполагается, что строки матрицы перенумерованы. Далее элементы матрицы перебираются по диагонали: сначала первый элемент первой строки, потом второй элемент второй строки и т.д. Выбранный элемент заменяется на какой-нибудь другой из допустимых a возможностей и далее утверждается, что таким образом построена строка, которой якобы нет в матрице (примеры см. в статьях «Теорема сегмента» и «Теорема отображений»).

При этом опять принимается aⁿ = n. Естественно, так как на самом деле aⁿ > n, то диагональный процесс никогда не охватывает всю матрицу; построенная в диагональном процессе строка ИМЕЕТСЯ в матрице, но только в той её части, которая не была охвачена диагональным процессом. Но кантористы считают, что получили строку, отличную от всех перенумерованных, и вместо естественного вывода о невозможности aⁿ = n делают фантастический вывод о невозможности перенумеровать строки матрицы.

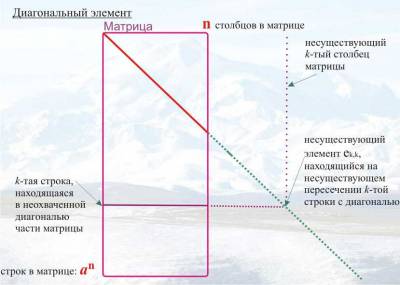
Третья разновидность диагонального метода в некотором роде противоположна предыдущей (Диаогональному процессу). Там по диагонали строилась строка, содержащаяся в неохваченной диагональю части матрицы (и утверждалось, что её нет в матрице). Здесь же в такой же матрице берется уже готовая строка из неохваченной диагональю части матрицы (строка k) и далее рассматривается элемент e_k,k, находящийся на пересечении строки k с диагональю. Так как строка k на самом деле с диагональю не пересекается (и, следовательно, элемент e_k,k не существует), то этот элемент e_k,k оказывается обладающим парадоксальными или противоречивыми свойствами.

Но опять же из этих противоречий не делается очевидный вывод о том, что  неверно предположение, будто aⁿ = n, (и, стало быть, что невозможно пересечение строки k с диагональю и существование элемента e_k,k), а делаются глобальные выводы совсем в другой области.

На отыскивании элемента e_k,k построены рассуждения в Теореме Гёделя, и в этом случае данный элемент представляет собой утверждение о недоказуемости самого этого утверждения в рассматриваемой аксиоматической системе, а глобальный вывод заключается в принципиальной неполноте любой формализованной аксиоматической системы (а в более общей интерпретации: человеческого логического мышления вообще).

На отыскивании элемента e_k,k построены также рассуждения в Теореме Тьюринга, и в её случае этот элемент представляет собой «машину Тьюринга» с противоречивыми свойствами, а глобальный вывод состоит в заключении о невозможности машины Тьюринга, решающей «проблему остановки» другой машины Тьюринга.

(В обоих случаях утверждения этих теорем, возможно, и верны, т.е., может быть, действительно всякая формализованная аксиоматическая система не обладает полнотой, и действительно невозможна машина Тьюринга, решающая проблему остановки других машин Тьюринга, но только способ, каким это «доказывается» при помощи Диагонального метода, ни в коем случае нельзя признать удовлетворительным, и эти проблемы требуют другого разбора и другой интерпретации).

Общим для всех трех вариантов Диагонального метода является то, что во всех случаях в исходной точке рассуждений принимается, что при бесконечном n будет иметь место равенство aⁿ = n и что элементы обоих множеств (aⁿ и n) можно свободно сопоставлять, поскольку ведь «они оба бесконечны», и разницу в их величине можно не принимать во внимание.

Это стартовое для всех рассуждений (по Диагональному методу) предположение в Веданской теории (ВТ) называется Постулатом Кантора. Постулат Кантора прямо вытекает из введенного Кантором же понятия взаимно однозначного соответствия (для бесконечных множеств).

Постулат Кантора даже «более постулат», чем многие другие постулаты (например, чем постулаты Эйнштейна в его СТО или чем постулаты ВТ), т.е. по форме и сущности более напоминает постулаты Евклида. Так, например, Третий постулат Евклида звучит: «Требуется, чтобы из всякого центра и всяким раствором можно было описать круг». Точно такую же необходимость в возможности выполнить некоторое действие провозглашает и Постулат Кантора: «Требуется, чтобы каждой строке матрицы можно было сопоставить её столбец» (или, в форме, пригодной также и для Стягивающихся интервалов: «Требуется, чтобы каждому элементу aⁿ можно было сопоставить элемент n»).

Без выполнения такого требования (т.е. без принятия Постулата Кантора) все рассуждения по Диагональному методу просто не могут быть даже начаты. Ведь если принять альтернативный постулат (что и при бесконечном n останется aⁿ > n) и принимать это обстоятельство во внимание, то все рассуждения Диагонального метода становятся очевидно бессмысленными.

Неодинаковые бесконечности

Таким образом, сущность всего происходящего вокруг Диагонального метода состоит в следующем.

1) Принимается Постулат Кантора, объявляющий, что «в бесконечности» будет иметь место aⁿ = n. Такой постулат противоречит духу всей предыдущей, доканторовской математики, в которой по правилу Лопиталя предел соотношения n / aⁿ при n → ∞ есть 0 и, следовательно, никакого соответствия между aⁿ и n установить нельзя. В доканторовской математике бесконечности не одинаковы, а Постулат Кантора первоначально объявляет их одинаковыми.

2) Однако потом при помощи Диагонального метода (если в силу принятия Постулата Кантора считать его рассуждения состоятельными) оказывается, что бесконечности всё-таки не одинаковы – и начинается построение хитроумного здания из этих всё-таки-не-одинаковых бесконечностей – но не того здания неодинаковых бесконечностей, которое имелось в доканторовской математике при правиле Лопиталя, а совсем другого, причудливого и (в отличие от здания доканторовских неодинаковых бесконечностей) уже не соответствующего никакой реальности.

В таком случае мы спрашиваем: зачем вообще нужно было принимать Постулат Кантора об одинаковости бесконечностей, если бесконечности всё равно оказываются неодинаковыми? Зачем всё это построение на основе произвольного и явно лишнего (по «Лезвию Оккама») постулата?

Ведь таких произвольных постулатов можно принимать сколько угодно и какие угодно. Можно постулировать, например, что 2/3 русалок белые, а 1/3 голубые, и на этой основе (добавив еще несколько постулатов такого же качества) строить «Теорию русалок». Эта «теория» будет иметь такую же ценность, как и «Канторовская теория множеств» (и с таким же правом считаться – или не считаться – частью математики).

Но задача науки состоит в Минимизации постулатов.

Диагональный метод и ВТ

Несостоятельность Диагонального метода и построенного на его основе Канторизма в общем-то видна и без ВТ (т.е. без привлечения аргументов из области теории интеллекта, представляющего собой продукт информатических систем). Для того, чтобы убедиться в этой несостоятельности, достаточно просто владеть доканторовской математикой (в первую очередь правилом Лопиталя) и ставить проблемы четко и ясно. (Канторизм вообще может существовать только при сохранении тумана в рассуждениях).

Однако ВТ дает сильную опору подлинной науке в противостоянии Канторизму. Ведь если интеллект представляет собой работу программ (как это утверждает Второй постулат ВТ), то в интеллекте (и, следовательно, в математике) может существовать только то, что возможно в «мире программ». И состоятельность Диагонального метода в этом мире невозможна.